PD Notation

The planar diagram (PD) notation for an oriented link may be obtained from a diagram as follows. First, label its edges from 1 to n, where n is the number of edges. Choose a first component and a starting edge, labeled 1. Label subsequent edges of the component in order according to its orientation. When this is done, choose a second component and an edge to label k+1 (if the first component had k edges). Continue until all the edges have been labeled.

Second, choose a component (not necessarily the first as chosen above) and crossing in which that component appears as an undercrossing. Assign an ordered 4-tuple (denoted {a,b,c,d} here) to this crossing by listing the valent edges of the crossing in counterclockwise order, beginning with the incoming lower edge. Repeat for subsequent undercrossings of this component (in order according to its orientation) to obtain an ordered list of m 4-tuples, where m is the number of times it is an undercrossing. Repeat for the other components (the order is arbitrary; it does not have to match the order in which the components were originally labeled).

Example

We apply the above method to assign a PD notation to the oriented link L4a1{0} (see figure below). We label the edges from 1 to 8 by choosing the blue component first and choosing the starting points on the first and second components at 1 and 5 as shown, respectively. Next we choose a crossing where purple crosses under blue; it is labeled {6,1,7,2} according to the convention above. The next such crossing is {8,3,5,4}. Then, as blue crosses under purple at {2,5,3,6} and {4,7,1,8}, the PD notation we obtain is {{6,1,7,2}, {8,3,5,4}, {2,5,3,6}, {4,7,1,8}}. Note that the choices made in this example were tailor-made to agree with the PD notation for L4a1{0} as it appears here.

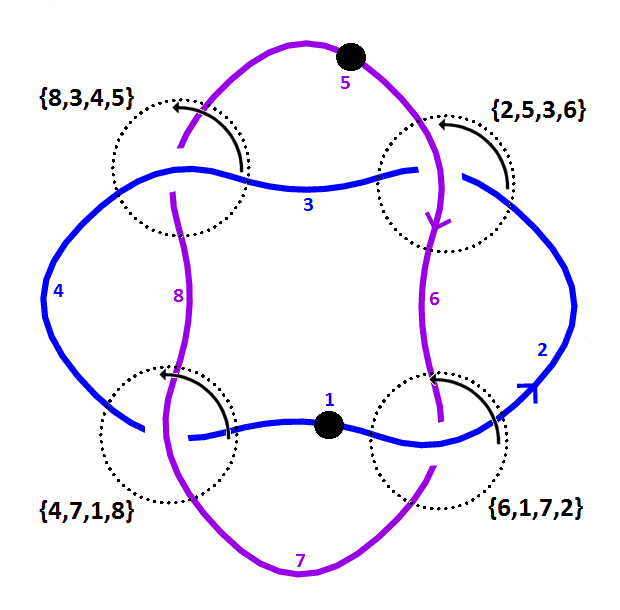
Remarks

An oriented link does not have a unique PD notation; however, one can recover an oriented link given a PD notation for it.

PD Notation (Math)

The computer program KnotTheory requires a slightly different format for PD Notation. For example, the PD notation for L4a1{0}, {{6,1,7,2},{8,3,5,4},{2,5,3,6},{4,7,1,8}}, becomes: PD[X[6,1,7,2],X[8,3,5,4],X[2,5,3,6],X[4,7,1,8]].