Conway Polynomial

The Conway Polynonial (or Alexander-Conway polynomial) Δ_L(z) of an oriented link L is given by det(z^1/2A - z^-1/2A^t), where A is a Seifert Matrix for L.

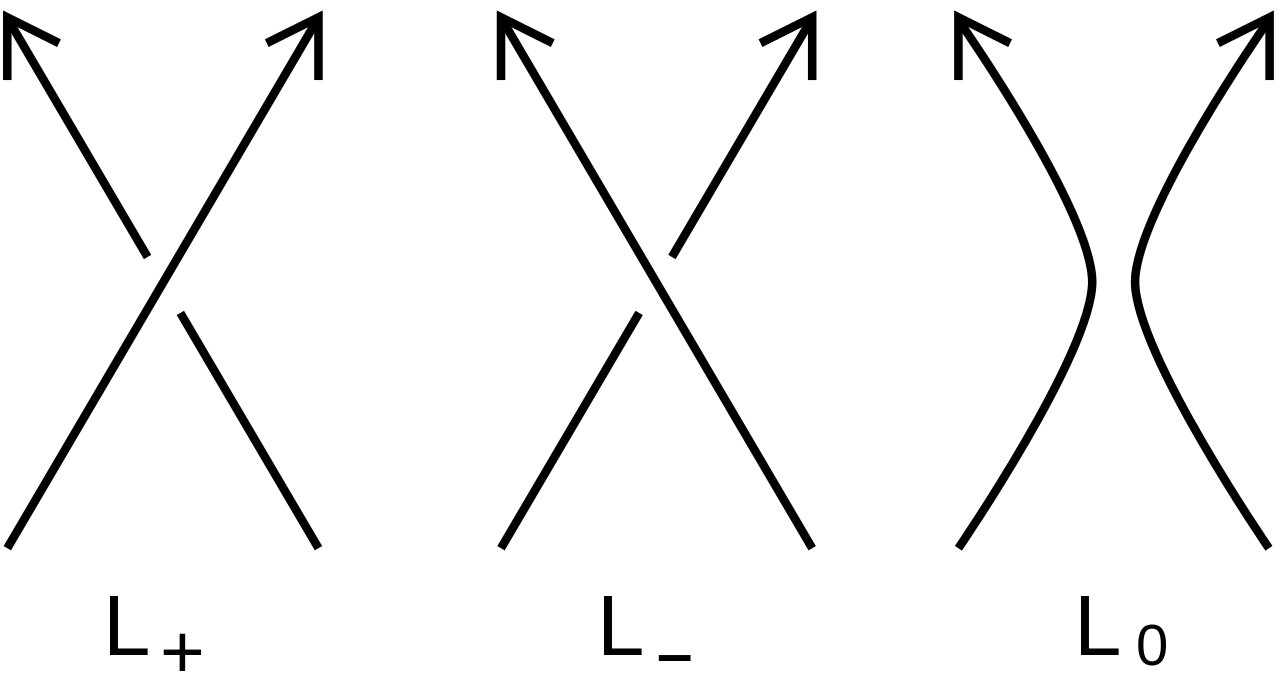
It can be shown that the Conway Polynomial is determined by the following skein relations:

(1) Δ_Unknot(z) = 1

(2) Δ_L₊(z) - Δ_{L_-}(z) = zΔ_L₀(z),

where L₊, L_-, and L₀ are three oriented links which are the same except in a neighborhood of a point where they differ as in the figure below.

Conway Polynomial Skein Relations

References

[1] Lickorish, W. B. R., An introduction to knot theory. New York: Springer (1997).

[2] Image taken from Wikipedia, The Free Encyclopedia. Alexander Polynomial.